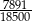Zadanie nr 6908755
Na osi liczbowej każde dwie spośród 1000 kolejnych liczb naturalnych 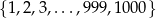 połączono odcinkiem. Następnie wybrano losowo jeden z tych odcinków. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że do wylosowanego odcinka należy liczba 307 (może też być jednym z jego końców). Wynik podaj w postaci ułamka nieskracalnego.
połączono odcinkiem. Następnie wybrano losowo jeden z tych odcinków. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że do wylosowanego odcinka należy liczba 307 (może też być jednym z jego końców). Wynik podaj w postaci ułamka nieskracalnego.
Rozwiązanie
Wszystkich odcinków o końcach w danych punktach jest
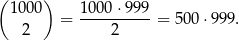
Sposób I
Jeżeli 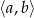 jest takim odcinkiem, że
jest takim odcinkiem, że 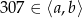 , to
, to 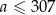 ,
, 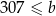 oraz
oraz 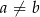 . Jest więc
. Jest więc
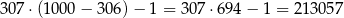
takich odcinków (lewy koniec wybieramy na 307 sposobów, prawy na 694 sposoby i odejmujemy zdegenerowany odcinek 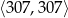 ). Interesujące nas prawdopodobieństwo jest więc równe
). Interesujące nas prawdopodobieństwo jest więc równe
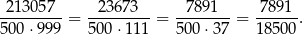
Otrzymany ułamek jest nieskracalny, bo łatwo sprawdzić, że liczba 7891 nie dzieli się przez żaden dzielnik mianownika, czyli przez żadną z liczb: 2, 5, 3, 37.
Sposób II
Zamiast obliczać liczbę odcinków, które zawierają 307, obliczmy ile jest odcinków, do których ta liczba nie należy. Końce takiego odcinka musimy wybrać z przedziału 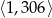 lub
lub 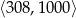 . Jest więc
. Jest więc
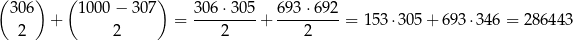
takich przedziałów i interesujące nas prawdopodobieństwo jest równe
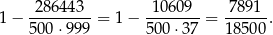
Otrzymany ułamek jest nieskracalny, bo łatwo sprawdzić, że liczba 7891 nie dzieli się przez żaden dzielnik mianownika, czyli przez żadną z liczb: 2, 5, 3, 37.
Odpowiedź: