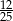Zadanie nr 7352754

Sześcian pomalowano, a następnie rozcięto na 1000 jednakowych sześcianików, które wrzucono do pudełka i wymieszano. Oblicz prawdopodobieństwo wylosowania z tego pudełka jednego, który:

będzie miał dwie ściany pomalowane;
będzie miał trzy ściany pomalowane;
będzie miał jedną lub dwie ściany pomalowane.

Rozwiązanie

Naszkicujmy sobie taki podział.

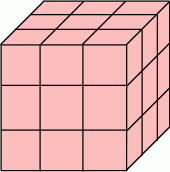
Na obrazku jest podział na 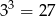33 = 27 sześcianików, w naszym podziale jest 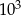10 3 sześcianików, czyli wzdłuż każdej krawędzi jest 10 sześcianów. Oczywiście mamy

|Ω | = 10 3.

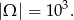
Sześcianiki z dwoma pomalowanymi ścianami to te, które były na krawędziach, ale nie w wierzchołkach. Przy każdej krawędzi jest 8 takich, czyli w sumie jest ich 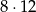i prawdopodobieństwo wynosi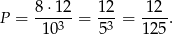
$8⋅12-- 12- -12- P = 103 = 5 3 = 125 .$

Odpowiedź: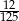
Tym razem chodzi o narożniki – jest ich 8, więc
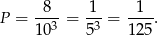
$-8-- -1- -1-- P = 103 = 5 3 = 125 .$

Odpowiedź:
Wiemy już, że jest 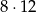sześcianików z dwoma pomalowanym i ścianami, pozostało policzyć te z jedną pomalowaną ścianą. Na każdej ścianie jest ich 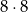(nie mogą dotykać krawędzi), czyli w sumie 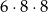. Prawdopodobieństwo wynosi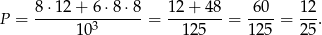
$P = 8-⋅12-+-6-⋅8-⋅8 = 1-2+--48 = -60- = 12. 103 1 25 1 25 25$

Odpowiedź: