/Szkoła średnia/Prawdopodobieństwo/Z definicji/Geometryczne

Zadanie nr 7749960

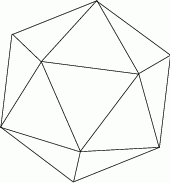
Każda ściana dwudziestościanu foremnego 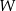W jest trójkątem równobocznym, a z każdego wierzchołka tej bryły wychodzi 5 krawędzi. Wybieramy losowo dwa różne wierzchołki wielościanu 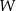W . Jakie jest prawdopodobieństwo tego, że odcinek łączący te dwa wierzchołki nie jest krawędzią wielościanu W ?

PIC

Wersja PDF

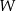Rozwiązanie

Obliczmy najpierw ile wierzchołków ma dwudziestościan foremny. Wiemy, że bryła ta ma 20 ścian i na każdej ścianie mamy 3 wierzchołki. Daje to nam 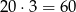20 ⋅3 = 6 0 wierzchołków, jednak każdy wierzchołek policzyliśmy w ten sposób 5 razy (bo jest na 5 ścianach). Zatem wierzchołków jest

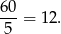
60- 5 = 1 2.

Podobnie możemy obliczyć liczbę krawędzi: 20 ścian trójkątnych daje 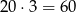20 ⋅3 = 6 0 krawędzi, ale każdą krawędź policzyliśmy 2 razy (bo każda krawędź jest na dwóch ścianach). Zatem wszystkich krawędzi jest

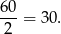
60 ---= 3 0. 2

Sposób I

Za zdarzenia elementarne przyjmijmy dwuelementowe zbiory wylosowanych wierzchołków, czyli

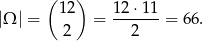
( 12) 12⋅ 11 |Ω | = = -------= 66. 2 2

Zamiast liczyć żądane prawdopodobieństwo, obliczmy prawdopodobieństwo zdarzenia przeciwnego. W takim zdarzeniu odcinek łączący wylosowane wierzchołki jest krawędzią wielościanu, a tych jak wiemy jest 30. Zatem

′ 30- 5-- ′ -5- -6- p = 66 = 11 ⇒ p = 1 − p = 1 − 11 = 11 .

Sposób II

Tym razem za zdarzenia elementarne przyjmijmy uporządkowane pary 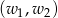(w 1,w 2) wylosowanych wierzchołków, czyli

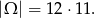
|Ω | = 12 ⋅11.

Liczymy zdarzenia sprzyjające. Pierwszy wierzchołek 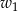w1 możemy wybrać dowolnie, ale wybierając drugi mamy już mniejszy wybór: nie może to być ani 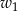w 1 , ani żaden z 5 sąsiadujących z nim wierzchołków. Wierzchołek 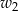w2 możemy więc dobrać do 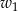w 1 na 6 sposobów. Zatem prawdopodobieństwo wynosi

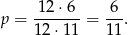
p = 1-2⋅6--= 6-. 12 ⋅11 11

 
Odpowiedź: 161

Wersja PDF