/Szkoła średnia/Prawdopodobieństwo/Z definicji/Geometryczne

Zadanie nr 8777500

Dodaj do ulubionych
Dodaj do rozwiązanych

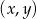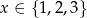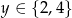Ze zbioru punktów o współrzędnych (x,y ) , gdzie x ∈ {1 ,2 ,3} zaś y ∈ {2,4} wybrano losowo dwa różne punkty. Oblicz prawdopodobieństwa zdarzeń:

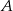  • A – wylosowane punkty należą do prostej o równaniu y = 2x ;
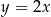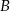  • B – wylosowane punkty są końcami odcinka równoległego do osi Ox .

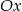Rozwiązanie

Pierwszą współrzędną losowanego punktu możemy wybrać na 3 sposoby, a drugą na 2, więc losujemy spośród

3⋅ 2 = 6

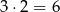
punktów. Jeżeli za zdarzenia elementarne przyjmiemy dwuelementowe zbiory wylosowanych punktów, to mamy

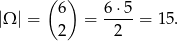
( ) |Ω | = 6 = 6-⋅5 = 1 5. 2 2
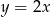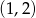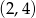  • W danym zbiorze punktów są tylko dwa punkty spełniające warunek y = 2x : są to (1,2) i (2,4) . Jest zatem jedno zdarzenie sprzyjające i prawdopodobieństwo wynosi P = 1- 15 .  
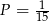    Odpowiedź: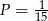 -1 P = 15
  • Podany warunek oznacza, że drugie współrzędne muszą być takie same. Dla ustalonej drugiej współrzędnej są 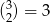(3) = 3 2 takie pary (wybieramy pierwsze współrzędne). W sumie jest więc 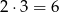2 ⋅3 = 6 takich par i prawdopodobieństwo wynosi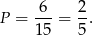
    6 2 P = ---= -. 15 5

     
    Odpowiedź: 2 5

Wersja PDF