/Szkoła średnia/Prawdopodobieństwo/Z definicji/Geometryczne

Zadanie nr 9161087

Każdą krawędź sześcianu kolorujemy jednym z 6 kolorów, wśród których są kolory: biały i czarny. Oblicz prawdopodobieństwo, że wśród pokolorowanych krawędzi są dokładnie 3 krawędzie białe i 2 czarne. Wynik podaj w postaci ułamka nieskracalnego.

Wersja PDF

Rozwiązanie

Sześcian ma 12 krawędzi, więc

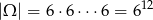
12 |Ω | = 6⋅ 6⋅⋅⋅6 = 6

(każdą z 12 krawędzi kolorujemy jednym z 6 kolorów).

W zdarzeniach sprzyjających mają być 3 krawędzie białe, ich położenie możemy wybrać na

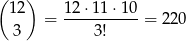
( ) 12 12-⋅11-⋅10- 3 = 3! = 220

sposobów.

Położenie krawędzi czarnych możemy wybrać na

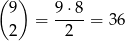
( 9) 9 ⋅8 = ---- = 3 6 2 2

sposobów. Na koniec każdą z pozostałych 7 krawędzi kolorujemy jednym z 4 pozostałych kolorów (nie możemy już używać ani białego, ani czarnego). W sumie jest więc

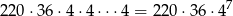
220 ⋅36 ⋅4 ⋅4⋅⋅⋅ 4 = 220 ⋅36 ⋅47

zdarzeń sprzyjających i prawdopodobieństwo wynosi

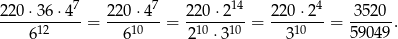
7 7 14 4 220-⋅36-⋅4--= 220⋅-4--= 22-0⋅2-- = 220-⋅2--= 35-20-. 612 610 210 ⋅310 310 59049

 
Odpowiedź: 539502049

Wersja PDF