Zadanie nr 9424020
Sześcian, którego ściany zostały pomalowane czerwoną farbą, dzielimy 6 płaszczyznami równoległymi do jego ścian na 27 identycznych sześcianików. Losujemy 2 spośród nich.
- Oblicz prawdopodobieństwo, że łączna liczba czerwonych ścian wylosowanych sześcianików wynosi 3.
- Oblicz prawdopodobieństwo, że wylosowane sześcianiki mają wspólną ścianę.
Rozwiązanie
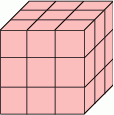
Za przestrzeń zdarzeń elementarnych przyjmijmy nieuporządkowane pary wylosowanych sześcianów. Mamy zatem
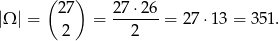
- Po opisanym podziale, mamy
8 sześcianów z 3 czerwonymi ścianami (naroża),
12 sześcianów z 2 czerwonymi ścianami (przy środkach krawędzi),
6 sześcianów z 1 czerwoną ścianą (środki ścian),
1 sześciań bez czerwonej ściany (środek sześcianu).
Mamy zatem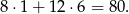
par sześcianów w których suma czerwonych ścian wynosi 3. Szukane prawdopodobieństwo wynosi zatem
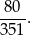
Odpowiedź: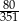
- Musimy starannie policzyć ilość par, które mają sąsiednią ścianę.
- Jeżeli jeden z sześcianów jest narożnikiem, to drugi można dobrać na 3 sposoby. Razem mamy
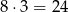 takie konfiguracje.
takie konfiguracje. - Jeżeli jeden z sześcianików jest w środku sześcianu, to drugi można dobrać na 6 sposobów. Mamy więc 6 takich konfiguracji.
- Pozostały jeszcze konfiguracje, w których jeden z sześcianów jest środkiem ściany, a drugi jest przy środku krawędzi. Jest
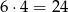 takich par.
takich par.
Razem mamy więc
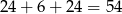 zdarzenia sprzyjające. Stąd
zdarzenia sprzyjające. Stąd 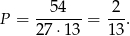
Odpowiedź: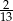
- Jeżeli jeden z sześcianów jest narożnikiem, to drugi można dobrać na 3 sposoby. Razem mamy

