Zadanie nr 9710477
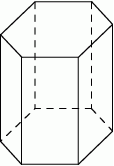
Spośród wierzchołków graniastosłupa sześciokątnego prostego losujemy jeden wierzchołek z dolnej podstawy i jeden wierzchołek z górnej podstawy. Oblicz prawdopodobieństwo tego, że wylosowane wierzchołki są końcami krawędzi bocznej graniastosłupa.
Rozwiązanie
Wierzchołek górnej podstawy możemy wybrać na 6 sposobów, wierzchołek dolnej podstawy też wybieramy na 6 sposobów. Zatem jest
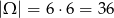
możliwości wybrania tych wierzchołków. Zdarzeń sprzyjających jest tyle, ile krawędzi bocznych, czyli 6. Prawdopodobieństwo jest więc równe
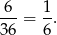
Odpowiedź: