Zadanie nr 3363717
Strzelając do tarczy pewien strzelec uzyskuje co najmniej 9 punktów z prawdopodobieństwem 0,5, a co najwyżej 9 punktów z prawdopodobieństwem 0,7. Oblicz prawdopodobieństwo, że ten strzelec uzyska dokładnie 9 punktów.
Rozwiązanie
Jeżeli oznaczymy przez 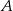 zdarzenie polegające na uzyskaniu co najmniej 9 punktów, a przez
zdarzenie polegające na uzyskaniu co najmniej 9 punktów, a przez 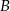 zdarzenie polegające na uzyskaniu co najwyżej 9 punktów, to mamy
zdarzenie polegające na uzyskaniu co najwyżej 9 punktów, to mamy 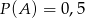 i
i 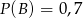 . To co mamy obliczyć, to dokładnie
. To co mamy obliczyć, to dokładnie 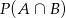 . Skorzystamy ze wzoru
. Skorzystamy ze wzoru
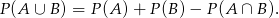
Zanim to jednak zrobimy zauważmy, że 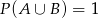 , bo zdarzenia
, bo zdarzenia 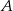 i
i 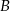 wyczerpują wszystkie możliwe wyniki jakie może uzyskać strzelec. Mamy więc
wyczerpują wszystkie możliwe wyniki jakie może uzyskać strzelec. Mamy więc
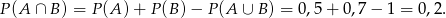
Odpowiedź: 0,2

