/Szkoła średnia/Prawdopodobieństwo/Z definicji/Różne

Zadanie nr 5169221

Mamy 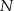N pałek o jednakowej długości. Każdą z nich łamiemy na 2 części: długą i krótką. 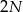2N części połączono losowo w 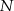N par, z których utworzono nowe pałki. Wyznacz prawdopodobieństwo tego, że:

  • części zostaną połączone tak, jak przed złamaniem;
  • wszystkie długie części będą połączone z krótkimi.
Wersja PDF

Rozwiązanie

Na początek policzmy na ile sposobów można połamane pałki połączyć w pary.

Bierzemy pierwszą z brzegu pałkę. Można do niej dobrać sąsiada na 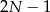2N − 1 sposobów.

Teraz z pozostałych pałek znowu wybieramy dowolną pałkę, można do niej dobrać sąsiada na 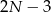2N − 3 sposobów.

Kontynuujemy tę procedurę aż zostaną dwie części. W sumie mamy więc

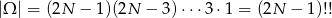
|Ω | = (2N − 1)(2N − 3)⋅⋅⋅3 ⋅1 = (2N − 1)!!

możliwości. Napisany symbol 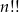n!! należy rozumieć tak jak jest napisane, czyli jako iloczyn liczb od 1 do n , biorąc co drugą liczbę.

  • Oczywiście jest dokładnie jedno zdarzenie sprzyjające, więc
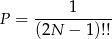
    P = ----1------ (2N − 1)!!

     
    Odpowiedź: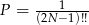 ---1---- P = (2N− 1)!!

  • Tym razem krótkie części (lub długie, wszystko jedno) mogą być dowolnie permutowane, więc jest 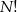N ! zdarzeń sprzyjających.  
    Odpowiedź: ---N!--- P = (2N− 1)!!
Wersja PDF