Rzucamy jednocześnie kostką i sześcioma symetrycznymi monetami. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, liczba otrzymanych oczek na kostce jest równa łącznej liczbie otrzymanych orłów na monetach.
Za zdarzenia elementarne przyjmijmy ciągi otrzymanych oczek/reszek/orłów. Wszystkich możliwych zdarzeń jest
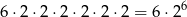
(sześć możliwych wyników na kostce i po dwa możliwe wyniki na każdej z monet).
Zastanówmy się teraz jak wyglądają zdarzenia sprzyjające. Zauważmy, że łącznie na monetach możemy otrzymać od 0 do 6 orłów i jeżeli liczba orłów nie jest równa 0, to liczbę oczek na kostce mamy już jednoznacznie wyznaczoną. Zdarzeń sprzyjających jest więc tyle, ile wszystkich możliwych wyników na monetach, w których jest co najmniej jeden orzeł. Takich zdarzeń jest
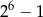
(od wszystkich możliwych wyników na monetach odejmujemy zdarzenie, w którym są same reszki). Interesujące nas prawdopodobieństwo jest więc równe
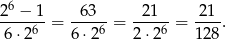
Odpowiedź: 
Informacje
Zadania
Losowe zadanie
