Zadanie nr 8068188
Na trzy półki kładziemy losowo 5 książek. Jakie jest prawdopodobieństwo tego, że jedna (i tylko jedna) z półek zostanie pusta?.
Rozwiązanie
Za zdarzenia elementarne przyjmijmy ciągi numerów półek, na które trafiają kolejne książki. Mamy zatem
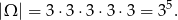
Sposób I
Półkę, która ma być pusta możemy wybrać na 3 sposoby. Gdy to jest ustalone, to książki możemy ustawić na dwóch półkach na
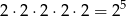
sposobów. Nie wszystkie z tych ustawień są jednak dobre, bo na każdej z tych dwóch ustalonych półek ma być przynajmniej jedna książka. Dlatego musimy odjąć złe ustawienia, które są dwa: odpowiadają one sytuacjom, gdy wszystkie książki trafiają na jedną półkę. W sumie jest więc
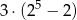
zdarzeń sprzyjających i prawdopodobieństwo jest równe
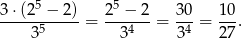
Sposób II
Tak jak poprzednio zaczynamy od ustalenia półki, która ma być pusta – możemy to zrobić na 3 sposoby. Pozostałe dwie półki mają być zajęte, więc muszą być na nich 3 i 2, lub 4 i 1 książki. Półkę na której ma być więcej książek wybieramy na 2 sposoby. Pozostało ustalić na ile sposobów można na niej umieścić książki. W wariancie 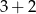 możemy to zrobić na
możemy to zrobić na
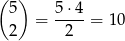
sposobów, a w wariancie 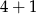 na
na
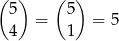
sposobów. W sumie jest więc
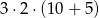
zdarzeń sprzyjających i prawdopodobieństwo jest równe
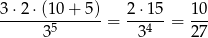
Odpowiedź: