Zadanie nr 8316987
Mamy 10 książek, wśród których są książki 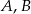 i
i 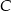 . Ustawiamy je losowo na pustej półce. Oblicz prawdopodobieństwo, że książki
. Ustawiamy je losowo na pustej półce. Oblicz prawdopodobieństwo, że książki 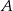 i
i 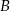 będą stały obok siebie w dowolnym porządku, natomiast
będą stały obok siebie w dowolnym porządku, natomiast 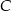 nie będzie sąsiadować z żadną z nich.
nie będzie sąsiadować z żadną z nich.
Rozwiązanie
Wszystkich możliwych ustawień jest
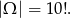
Policzymy ile jest zdarzeń sprzyjających, przy czym założymy, że najpierw stoi 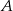 , potem
, potem 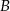 - na koniec otrzymany wynik pomnożymy przez dwa, co będzie odpowiadać zamianie
- na koniec otrzymany wynik pomnożymy przez dwa, co będzie odpowiadać zamianie 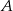 i
i 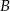 . Skoro
. Skoro 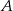 i
i 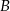 stoją obok siebie, będziemy krótko mówić o parze
stoją obok siebie, będziemy krótko mówić o parze 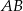 . Parę tę możemy postawić na półce na 9 sposobów (na pozycjach
. Parę tę możemy postawić na półce na 9 sposobów (na pozycjach 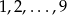 ). Łatwo teraz zauważyć (np. na rysunku), że jak
). Łatwo teraz zauważyć (np. na rysunku), że jak 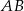 stoją na brzegu (na pozycji 1 lub 9), to
stoją na brzegu (na pozycji 1 lub 9), to 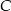 można postawić na 7 sposobów (są tylko trzy pola spalone). Pozostałe książki stawiamy dowolnie, więc jest
można postawić na 7 sposobów (są tylko trzy pola spalone). Pozostałe książki stawiamy dowolnie, więc jest
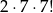
takich konfiguracji. Jeżeli para 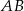 stoi w środku (co może się zdarzyć na 9-2=7 sposobów), to są cztery spalone pola, co daje 6 możliwości dla
stoi w środku (co może się zdarzyć na 9-2=7 sposobów), to są cztery spalone pola, co daje 6 możliwości dla 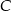 i mamy
i mamy
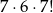
konfiguracji. Zatem prawdopodobieństwo wynosi
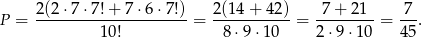
Odpowiedź: