/Szkoła średnia/Prawdopodobieństwo/Z definicji/Różne

Zadanie nr 9779554

Dodaj do ulubionych
Dodaj do rozwiązanych

Wybieramy losowo 2 kostki z tabliczki czekolady przedstawionej na poniższym rysunku.

PIC

Oblicz prawdopodobieństwo tego, że wybrane dwie kostki są sąsiednie (tzn. mają wspólną krawędź).

Rozwiązanie

Przyjmijmy za zdarzenia elementarne nieuporządkowane pary wylosowanych kostek.

Sposób I

Wszystkich zdarzeń elementarnych jest

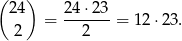
( ) 24 2-4⋅23- 2 = 2 = 12 ⋅23.

Zdarzenia sprzyjające, czyli pary sąsiednich kostek są dwóch rodzajów: poziome i pionowe. Poziomych jest

4 ⋅5 = 20

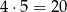
(po 5 w każdym poziomym rzędzie), a pionowych jest

6 ⋅3 = 18

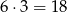
(po 3 w każdym pionowym rzędzie). Interesujące nas prawdopodobieństwo jest więc równe

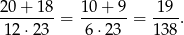
20+ 18 10+ 9 19 --------= -------= ----. 12 ⋅23 6 ⋅23 1 38

Sposób II

Tym razem obliczmy liczbę zdarzeń elementarnych tak, aby nie korzystać z symbolu Newtona.

Pierwszą kostkę możemy wybrać na 24, a drugą 23 sposoby. W ten sposób liczymy jednak każdą parę kostek podwójnie, bo nie chcemy zwracać uwagi na to, która kostka jest pierwsza, a która druga. Jest więc

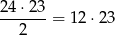
24-⋅23- 2 = 12 ⋅23

możliwości wybrania dwóch kostek.

Zdarzenia sprzyjające i prawdopodobieństwo obliczamy tak samo jak w I sposobie.  
Odpowiedź: -19 138

Wersja PDF