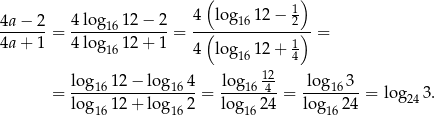Zadanie nr 2745832

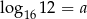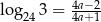Wykaż, że jeżeli log 1612 = a , to 4a−-2 lo g243 = 4a+ 1 .

Rozwiązanie

Będziemy korzystać ze wzoru na zmianę podstawy logarytmu

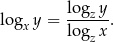
log y logx y = ----z-. logz x

Sposób I

Zauważmy, że dany warunek możemy zapisać w postaci

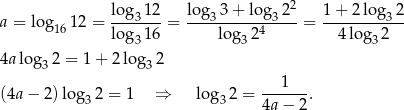
log 12 lo g 3 + log 22 1+ 2 log 2 a = log 16 12 = ----3-- = ---3-------3----= --------3--- log 316 log3 24 4log3 2 4a lo g 2 = 1+ 2 log 2 3 3 (4a − 2) log 2 = 1 ⇒ log 2 = ---1---. 3 3 4a − 2

Przekształcamy teraz lewą stronę równości, którą mamy udowodnić – zamieniamy podstawę logarytmu na 3.

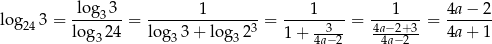
-log-33- -------1-------- ----1---- ---1--- 4a-−--2 log243 = log 2 4 = log 3 + log 2 3 = 1 + --3- = 4a−2+-3 = 4a + 1 3 3 3 4a−2 4a− 2

Sposób II

Przekształcamy prawą stronę wzoru, który mamy udowodnić.

( ) 4 lo g 12 − 1 4a-−-2-= 4log-1612-−-2-= -(----16-----2)--= 4a + 1 4log 1612 + 1 4 lo g 12 + 1 16 4 log 12 − log 4 lo g 12 log 3 = ---16---------16-- = ---16-4-= ----16---= log243. log1612 + log 16 2 log 1624 log1624