Zadanie nr 3303622
Udowodnij, że jeśli liczby dodatnie  i
i 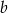 spełniają warunek
spełniają warunek 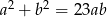 , to
, to 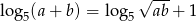 .
.
Rozwiązanie
Podany warunek możemy zapisać w postaci
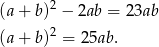
Teraz logarytmujemy tę równość logarytmem przy podstawie 5.
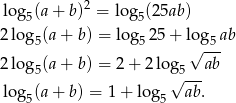
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Udowodnij, że jeśli liczby dodatnie  i
i 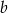 spełniają warunek
spełniają warunek 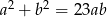 , to
, to 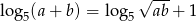 .
.
Podany warunek możemy zapisać w postaci
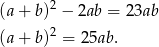
Teraz logarytmujemy tę równość logarytmem przy podstawie 5.