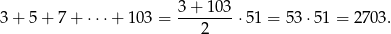/Szkoła średnia/Liczby/Logarytmy/Tożsamości

Zadanie nr 5705963

Dodaj do ulubionych
Dodaj do rozwiązanych

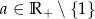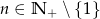Udowodnij, że dla a ∈ R + ∖{1 } oraz n ∈ N + ∖ {1} spełniona jest równość:

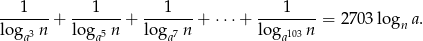
---1---+ ---1---+ ---1---+ ⋅ ⋅⋅+ ----1--- = 2703 lo g a. loga3 n loga5 n loga7 n loga103 n n

Rozwiązanie

Przekształcamy lewą stronę równości zmieniając podstawy wszystkich logarytmów na n .

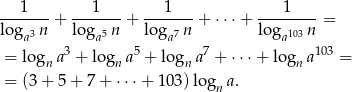
---1---+ ---1---+ --1----+ ⋅⋅⋅ + ----1--- = loga3 n lo ga5 n lo ga7 n loga103 n = log a3 + log a5 + log a7 + ⋅ ⋅⋅+ log a103 = n n n n = (3 + 5+ 7+ ⋅⋅⋅+ 1 03)logn a.

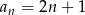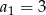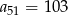Suma liczb w nawiasie to suma kolejnych wyrazów ciągu arytmetycznego a = 2n + 1 n . Mamy a = 3 1 i a = 103 51 , więc jest to suma 51 wyrazów tego ciągu. Zatem

3+ 103 3 + 5 + 7 + ⋅⋅⋅+ 103 = --------⋅51 = 53 ⋅51 = 2703. 2
Wersja PDF