Zadanie nr 7085767
Uzasadnij, że 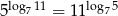 .
.
Rozwiązanie
Sposób I
Spróbujmy przekształcić lewą stronę tak, aby dojść do prawej.
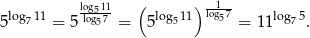
Na końcu skorzystaliśmy z tego, że
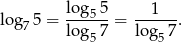
Sposób II
Przekształcamy równość, którą mamy udowodnić w sposób równoważny – logarytmujemy ją stronami logarytmem przy podstawie 7.
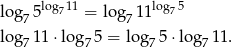
Otrzymana równość jest oczywiście prawdziwa, więc wyjściowa równość też musiała być prawdziwa (bo przekształcaliśmy przy pomocy równoważności).

