Zadanie nr 7297772
Dodatnie liczby rzeczywiste  i
i 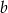 takie, że
takie, że 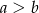 , spełniają warunek
, spełniają warunek
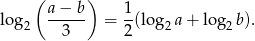
Wykaż, że dla liczb  i
i 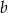 prawdziwa jest równość
prawdziwa jest równość 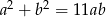 .
.
Rozwiązanie
Przekształcamy podany warunek
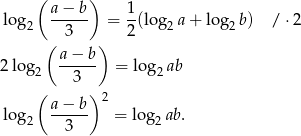
Ponieważ logarytm 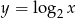 jest funkcją różnowartościową, mamy stąd
jest funkcją różnowartościową, mamy stąd
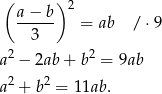
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dodatnie liczby rzeczywiste  i
i 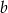 takie, że
takie, że 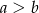 , spełniają warunek
, spełniają warunek
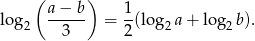
Wykaż, że dla liczb  i
i 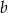 prawdziwa jest równość
prawdziwa jest równość 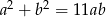 .
.
Przekształcamy podany warunek
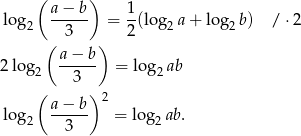
Ponieważ logarytm 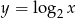 jest funkcją różnowartościową, mamy stąd
jest funkcją różnowartościową, mamy stąd