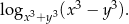Zadanie nr 9475703
Liczby rzeczywiste 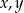 spełniają warunki:
spełniają warunki: 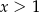 ,
, 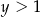 oraz
oraz 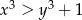 . Wykaż, że prawdziwa jest równość
. Wykaż, że prawdziwa jest równość
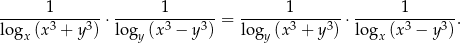
Rozwiązanie
Będziemy korzystać ze wzoru
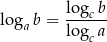
na zmianę podstawy logarytmu.
Sposób I
Przekształcamy daną równość w sposób równoważny – zmieniamy podstawy wszystkich logarytmów na  .
.
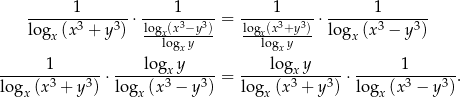
Otrzymana równość jest oczywiście prawdziwa, więc wyjściowa równość też musiała być spełniona (bo przekształcaliśmy ją w sposób równoważny).
Sposób II
Przekształcamy daną równość w sposób równoważny – zmieniamy podstawy wszystkich logarytmów na 10.
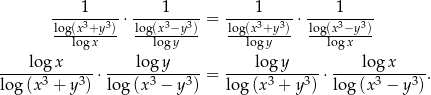
Otrzymana równość jest oczywiście prawdziwa, więc wyjściowa równość też musiała być spełniona (bo przekształcaliśmy ją w sposób równoważny).
Sposób III
Równość, którą mamy udowodnić możemy zapisać w postaci
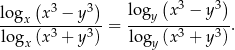
Na mocy wzoru na zmianę podstawy logarytmu, każda ze stron jest równa wyrażeniu