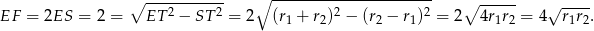Zadanie nr 1136830
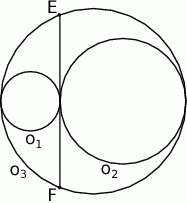
Dane są trzy okręgi  ,
,  i
i  . Okręgi
. Okręgi 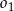 ,
, 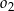 są styczne zewnętrznie, jednocześnie są styczne wewnętrznie do okręgu
są styczne zewnętrznie, jednocześnie są styczne wewnętrznie do okręgu 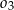 (patrz rysunek). Promienie okręgów
(patrz rysunek). Promienie okręgów 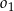 i
i 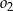 są odpowiednio równe
są odpowiednio równe 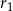 i
i 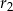 , a środki wszystkich trzech okręgów leżą na jednej prostej. Uzasadnij, że długość odcinka
, a środki wszystkich trzech okręgów leżą na jednej prostej. Uzasadnij, że długość odcinka 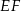 jest równa
jest równa 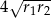 , gdzie odcinek
, gdzie odcinek 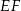 jest cięciwą okręgu
jest cięciwą okręgu 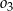 i zawiera się we wspólnej stycznej okręgów
i zawiera się we wspólnej stycznej okręgów 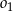 i
i 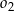 .
.
Rozwiązanie
Niech 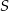 będzie punktem styczności okręgów
będzie punktem styczności okręgów 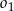 i
i 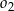 , a
, a 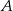 i
i 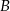 niech będą punktami styczności tych okręgów z okręgiem
niech będą punktami styczności tych okręgów z okręgiem 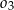 .
.
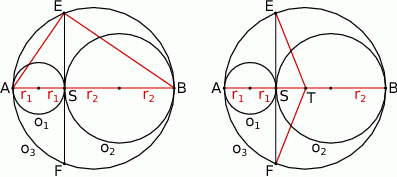
Sposób I
Wiemy, że środki wszystkich trzech okręgów leżą na jednej prostej, więc 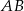 jest średnicą okręgu
jest średnicą okręgu 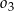 . W takim razie trójkąt
. W takim razie trójkąt 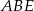 jest prostokątny. Prosta
jest prostokątny. Prosta 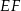 jako styczna do
jako styczna do 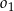 i
i 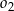 jest prostopadła do prostej łączącej środki tych okręgów, czyli do
jest prostopadła do prostej łączącej środki tych okręgów, czyli do 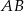 . W takim razie
. W takim razie 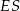 jest wysokością w trójkącie
jest wysokością w trójkącie 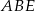 .
.
Aby obliczyć długość odcinka 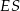 zauważmy, że trójkąty
zauważmy, że trójkąty 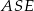 i
i 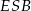 są podobne (bo każdy z nich jest podobny do trójkąta
są podobne (bo każdy z nich jest podobny do trójkąta 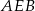 ). W takim razie
). W takim razie
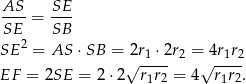
Sposób II
Korzystamy z tego, że wysokość opuszczona z wierzchołka kąta prostego trójkąta prostokątnego ma długość równą średniej geometrycznej długości odcinków, na które wysokość ta dzieli przeciwprostokątną. Mamy zatem
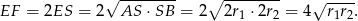
Sposób III
Tym razem patrzymy na trójkąt prostokątny 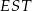 , gdzie
, gdzie 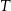 jest środkiem największego okręgu. Mamy w nim
jest środkiem największego okręgu. Mamy w nim
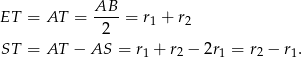
Korzystamy teraz z twierdzenia Pitagorasa