Zadanie nr 9839889
Do dwóch okręgów przecinających się w punktach 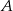 i
i 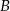 poprowadzono wspólną styczną
poprowadzono wspólną styczną 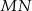 , przy czym punkt
, przy czym punkt 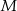 należy do pierwszego, a punkt
należy do pierwszego, a punkt 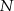 do drugiego okręgu. Wykaż, że prosta
do drugiego okręgu. Wykaż, że prosta 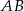 dzieli odcinek
dzieli odcinek 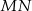 na połowy.
na połowy.
Rozwiązanie
Rozpoczynamy od rysunku.
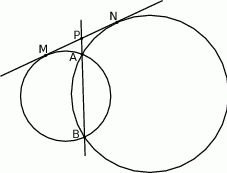
Jeżeli 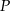 jest punktem wspólnym prostych
jest punktem wspólnym prostych 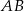 i
i 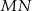 to na mocy twierdzenia o stycznej i siecznej mamy
to na mocy twierdzenia o stycznej i siecznej mamy
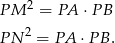
Zatem 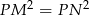 , czyli
, czyli 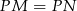 .
.

