/Konkursy/Zadania/Geometria/Planimetria/Okrąg i koło

Zadanie nr 3402896

Dodaj do ulubionych
Dodaj do rozwiązanych

Dane są cztery okręgi. Każdy z nich jest styczny zewnętrznie do dokładnie dwóch spośród trzech pozostałych okręgów. Udowodnij, że punkty styczności tych okręgów są wierzchołkami czworokąta, na którym można opisać okrąg.

Rozwiązanie

Zaczynamy od rysunku – od razu dorysujmy odcinki łączące środki danych okręgów.

PIC

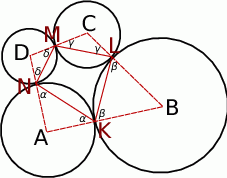
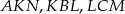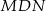Jeżeli oznaczymy kąty ostre trójkątów równoramiennych AKN ,KBL ,LCM i MDN jak na rysunku, to mamy

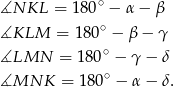
∘ ∡NKL = 180 − α − β ∡KLM = 18 0∘ − β− γ ∘ ∡LMN = 180 − γ − δ ∡MNK = 180∘ − α − δ.

Z tych równości łatwo widać, że

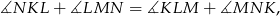
∡NKL + ∡LMN = ∡KLM + ∡MNK ,

co kończy dowód, bo jest to warunek wystarczający na to, żeby na czworokącie 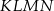KLMN dało się opisać okrąg.

Wersja PDF