Zadanie nr 3858768
W kole o środku 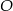 poprowadzono dwie prostopadłe średnice
poprowadzono dwie prostopadłe średnice 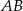 i
i 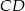 oraz cięciwę
oraz cięciwę 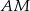 przecinającą średnicę
przecinającą średnicę 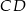 w punkcie
w punkcie 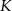 . Oblicz miarę kąta
. Oblicz miarę kąta 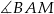 wiedząc, że w czworokąt
wiedząc, że w czworokąt 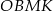 można wpisać okrąg.
można wpisać okrąg.
Rozwiązanie
Sposób I
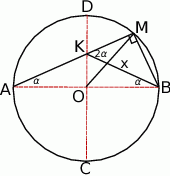
Zaczynamy od rysunku.
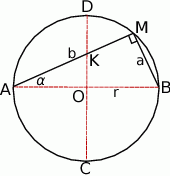
To, że w czworokąt 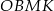 można wpisać okrąg oznacza, że
można wpisać okrąg oznacza, że
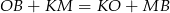
Najtrudniejsze w tym zadaniu to wymyślenie sposobu na wykorzystanie tej informacji. Jeżeli się jednak chwilę przyjrzymy, to trójkąt 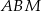 jest prostokątny (bo
jest prostokątny (bo 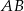 jest średnicą), więc w miarę łatwo powinno dać się powyliczać wszystkie odcinki biorące udział w powyższej równości.
jest średnicą), więc w miarę łatwo powinno dać się powyliczać wszystkie odcinki biorące udział w powyższej równości.
Oznaczmy 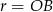 ,
, 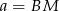 i
i 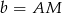 . Zauważmy, że trójkąt
. Zauważmy, że trójkąt 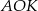 jest podobny do trójkąta
jest podobny do trójkąta 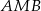 (bo też jest prostokątny i ma wspólny kąt z
(bo też jest prostokątny i ma wspólny kąt z 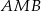 ). Zatem
). Zatem
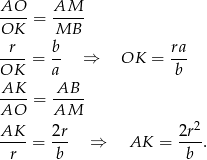
Możemy teraz zapisać równość z początku rozwiązania.
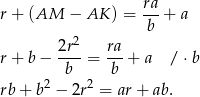
Ponieważ nie bardzo wiadomo co z tym dalej zrobić, zamienimy wszystko na 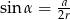 i
i 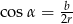 .
.
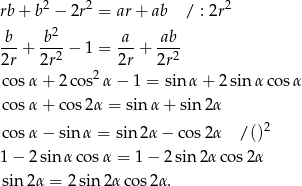
Jest jasne, że 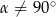 i
i 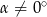 , czyli
, czyli 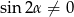 i mamy
i mamy
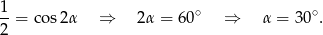
Sposób II
Powyższe rozwiązanie jest wprawdzie koncepcyjnie dość proste, ale rachunki nie były zbyt przyjemne, dlatego spróbujmy znaleźć prostszy sposób. Po pierwsze zauważmy, że okrąg wpisany w czworokąt 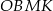 to po prostu okrąg wpisany w trójkąt
to po prostu okrąg wpisany w trójkąt 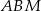 , zatem treść zadania można zamienić na trochę prostszą: okrąg wpisany w trójkąt prostokątny
, zatem treść zadania można zamienić na trochę prostszą: okrąg wpisany w trójkąt prostokątny 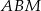 (
(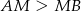 ) jest styczny do symetralnej przeciwprostokątnej
) jest styczny do symetralnej przeciwprostokątnej 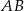 ; oblicz miarę kąta
; oblicz miarę kąta 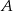 .
.
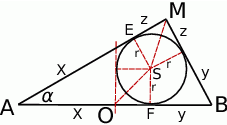
Jedyna rzecz jakiej będziemy potrzebować w rozwiązaniu to wzory na długości odcinków 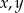 i
i  łączących wierzchołki trójkąta
łączących wierzchołki trójkąta 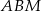 z punktami styczności boków z okręgiem wpisanym. Jeżeli oznaczymy standardowo
z punktami styczności boków z okręgiem wpisanym. Jeżeli oznaczymy standardowo 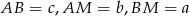 , to odcinki te spełniają układ równań
, to odcinki te spełniają układ równań
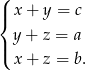
Odejmując od pierwszego równania drugie i do wyniku dodając trzecie dostaniemy
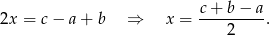
Stąd łatwo wyliczyć 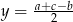 i
i 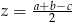 .
.
Jak już to wiemy to rowiązanie jest prawie natychmiastowe. Każdy z trójkątów prostokątnych 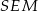 i
i 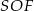 ma kąt ostry równy
ma kąt ostry równy 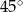 , są więc one równoramienne. Mamy zatem
, są więc one równoramienne. Mamy zatem
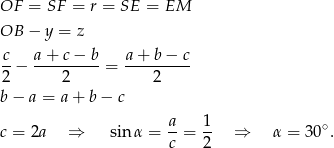
Sposób III
Tak jak w poprzednim sposobie zajmujemy się okręgiem wpisanym w trójkąt prostokątny 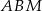 .
.
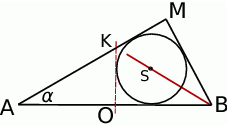
Zauważmy, że prosta 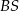 jest osią symetrii czworokąta
jest osią symetrii czworokąta 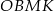 . Rzeczywiście, przy symetrii względem tej prostej styczna do okręgu
. Rzeczywiście, przy symetrii względem tej prostej styczna do okręgu 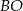 przejdzie na styczną do okręgu, czyli na
przejdzie na styczną do okręgu, czyli na 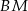 . Ponadto prosta
. Ponadto prosta 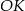 , która jest prostopadła do
, która jest prostopadła do 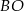 i styczna do okręgu przejdzie na prostopadłą do
i styczna do okręgu przejdzie na prostopadłą do 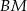 i styczną do okręgu, czyli na
i styczną do okręgu, czyli na 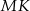 . To w szczególności oznacza, że
. To w szczególności oznacza, że 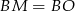 . Stąd
. Stąd
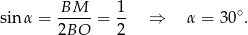
Sposób IV
Tym razem wróćmy do oryginalnego sformułowania i oznaczmy 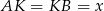 .
.
Wyliczymy wszystkie boki czworokąta 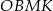 w zależności od
w zależności od  i
i  . Trójkąt
. Trójkąt 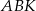 jest równoramieny więc
jest równoramieny więc
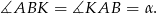
Stąd
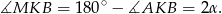
Patrząc na trójkąty prostokątne 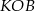 i
i 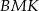 łatwo wyliczyć boki czworokąta
łatwo wyliczyć boki czworokąta 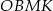 .
.
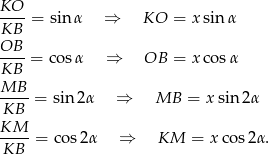
Jeżeli teraz napiszemy warunek równości przeciwległych boków czworokąta 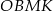 to mamy
to mamy
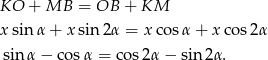
Równanie to rozwiązujemy dokładnie tak samo jak w sposobie I.
Odpowiedź: