/Szkoła średnia/Statystyka/Dane z wykresu

Zadanie nr 2268121

Dodaj do ulubionych
Dodaj do rozwiązanych

W pewnym liceum, wśród uczniów 30 osobowej klasy (każdy uczeń pochodzi z innej rodziny), zebrano dane na temat posiadanego rodzeństwa. Wyniki badań przedstawiono na diagramie.

PIC

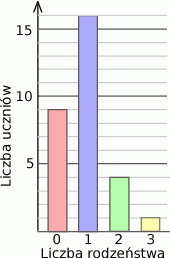
  • Wychowawczyni wybrała 3 osoby z tej klasy. Oblicz prawdopodobieństwo, że jedna z nich ma dwoje rodzeństwa, a dwie pozostałe nie mają rodzeństwa. Wynik zaokrąglij do części setnych.
  • Oblicz średnią liczbę dzieci w jednej badanej rodzinie, odchylenie standardowe i medianę.

Rozwiązanie

  • Obliczmy na ile sposobów można wybrac 3 osoby z 30.
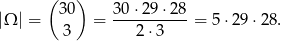
    ( ) 30 30-⋅29-⋅28- |Ω | = 3 = 2 ⋅3 = 5 ⋅29 ⋅28.

    Osobę z dwojgiem rodzeństwa można wybrać na 4 sposoby, a osobę bez rodzeństwa na 9 sposobów. Jest zatem

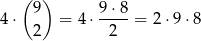
    ( ) 9 9-⋅8 4⋅ 2 = 4 ⋅ 2 = 2⋅9 ⋅8

    zdarzeń sprzyjających. Zatem prawdopodobieństwo wynosi

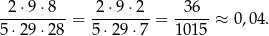
    -2-⋅9-⋅8- 2-⋅9-⋅2- -36-- 5 ⋅29 ⋅28 = 5⋅ 29⋅7 = 101 5 ≈ 0,04 .

     
    Odpowiedź: 0,04

  • Zauważmy, że podane dane mówią o liczbie rodzeństwa pytanych dzieci. Liczba dzieci w każdej rodzinie jest o 1 większa.

    Liczymy średnią

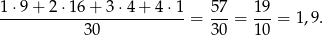
    1⋅9 + 2 ⋅16 + 3 ⋅4+ 4⋅ 1 57 19 --------------------------= ---= ---= 1,9. 30 30 10

    Liczymy teraz odchylenie standardowe

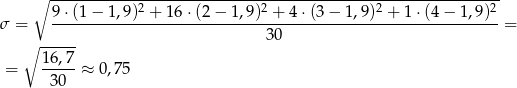
    ∘ -------------------------------------------------------------- 9 ⋅(1 − 1,9)2 + 16 ⋅(2− 1,9)2 + 4⋅(3 − 1 ,9 )2 + 1 ⋅(4 − 1,9)2 σ = ------------------------------------------------------------- = ∘ ----- 30 16,7- = 30 ≈ 0,75

    Ponieważ badanie przeprowadzono wśród 30 dzieci, mediana jest średnią arytmetyczną 15 i 16 danej. Obie te dane są równe 2, więc mediana jest równa 2.  
    Odpowiedź: Średnia: 1,9, odchylenie: 0,75, mediana: 2

Wersja PDF