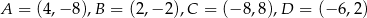Zadanie nr 1373538
Punkty 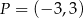 ,
, 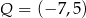 i
i 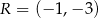 są środkami odpowiednio boków
są środkami odpowiednio boków 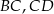 i
i 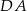 równoległoboku
równoległoboku 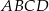 . Wyznacz współrzędne wierzchołków tego równoległoboku.
. Wyznacz współrzędne wierzchołków tego równoległoboku.
Rozwiązanie
Szkicujemy opisaną sytuację.
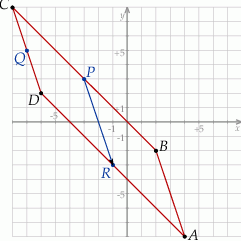
Mamy
![−→ −→ −→ BA = CD = P R = [− 1 + 3,− 3 − 3] = [2,− 6].](https://img.zadania.info/zad/1373538/HzadR1x.gif)
To pozwala łatwo wyznaczyć współrzędne wierzchołków 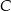 i
i 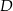
![1-−→ D = Q + 2CD = (− 7,5) + [1,− 3] = (− 6,2) − → −→ Q = C + 1CD ⇒ C = Q − 1-CD = (− 7 ,5 )− [1,− 3] = (− 8,8). 2 2](https://img.zadania.info/zad/1373538/HzadR4x.gif)
Współrzędne punktów 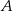 i
i 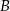 wyznaczamy z tego, że
wyznaczamy z tego, że 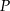 i
i 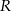 są środkami odcinków
są środkami odcinków 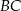 i
i 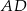 .
.
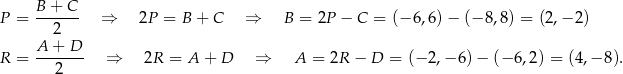
Odpowiedź: