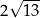/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt/Równoległobok

Zadanie nr 1892157

Dodaj do ulubionych
Dodaj do rozwiązanych

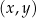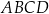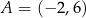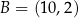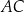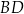W kartezjańskim układzie współrzędnych (x,y ) dany jest równoległobok ABCD , w którym A = (− 2,6) oraz B = (10 ,2 ) . Przekątne AC oraz BD tego równoległoboku przecinają się w punkcie 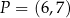P = (6 ,7) . Oblicz długość boku 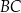BC tego równoległoboku.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

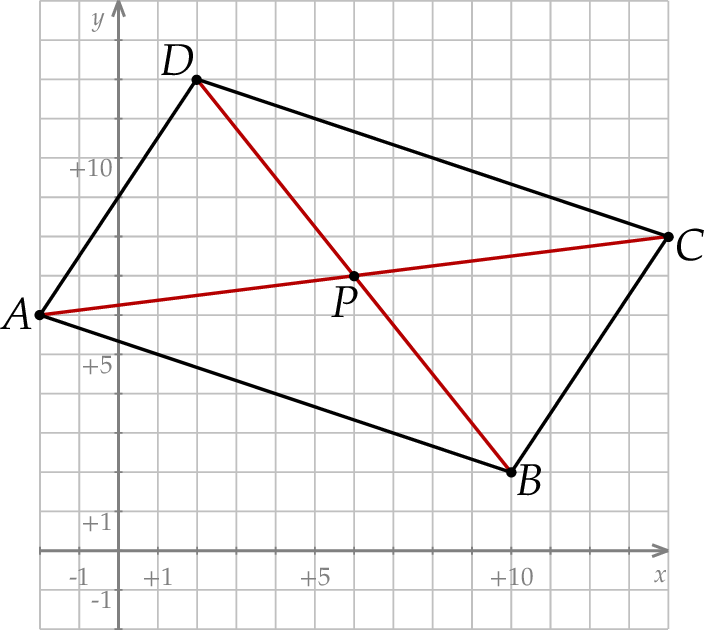
ZINFO-FIGURE

Przekątne równoległoboku dzielą się na połowy, więc punkt przecięcia się przekątnych 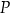P to środek odcinka 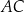AC , czyli

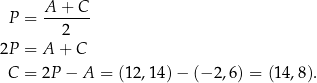
A-+--C- P = 2 2P = A + C C = 2P − A = (12 ,14)− (− 2,6) = (14,8).

Stąd

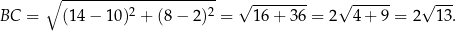
∘ ---------------------- 2 2 √ -------- √ ------ √ --- BC = (14 − 10) + (8 − 2) = 1 6+ 3 6 = 2 4 + 9 = 2 13.

 
Odpowiedź: √ --- 2 13

Wersja PDF