Zadanie nr 7923031
Punkt 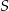 jest punktem przecięcia się przekątnych równoległoboku
jest punktem przecięcia się przekątnych równoległoboku 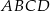 , a punkt
, a punkt 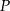 jest takim punktem boku
jest takim punktem boku 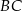 tego równoległoboku, że
tego równoległoboku, że 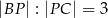 . Oblicz współrzędne spodka wysokości opuszczonej z wierzchołka
. Oblicz współrzędne spodka wysokości opuszczonej z wierzchołka 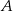 tego równoległoboku na prostą
tego równoległoboku na prostą 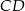 , jeżeli
, jeżeli ![−→ AB = [4,4]](https://img.zadania.info/zad/7923031/HzadT7x.gif) ,
, ![−→ DS = [3,− 3]](https://img.zadania.info/zad/7923031/HzadT8x.gif) i
i 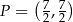 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
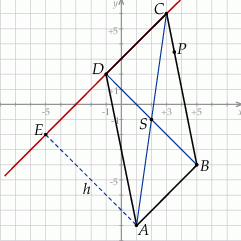
Obliczymy najpierw współrzędne wierzchołków równoległoboku. Zauważmy, że
![−→ −→ −→ −→ → −→ −→ BC = BD + DC = 2SD + AB = − 2DS + AB = = − 2[3,− 3]+ [4,4] = [− 2,1 0].](https://img.zadania.info/zad/7923031/HzadR1x.gif)
Wiemy ponadto, że punkt 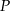 dzieli odcinek
dzieli odcinek 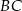 w stosunku 3:1, więc
w stosunku 3:1, więc
![[ ] −→ 1-−→ 1- 1-5- PC = 4 BC = 4 [− 2,10 ] = − 2,2 .](https://img.zadania.info/zad/7923031/HzadR4x.gif)
Teraz łatwo już wyznaczyć współrzędne wierzchołka 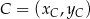 .
.
![[ ] [ ] 1-5- −→ 7- 7- − 2,2 = PC = xC − 2,yC − 2 ⇒ C = (xC,yC ) = (3,6).](https://img.zadania.info/zad/7923031/HzadR6x.gif)
Teraz korzystając ze współrzędnych wektorów 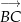 i
i 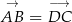 obliczamy współrzędne pozostałych wierzchołków równoległoboku.
obliczamy współrzędne pozostałych wierzchołków równoległoboku.
![−→ [− 2,10] = BC = [3 − xB,6 − yB ] ⇒ B = (xB ,yB) = (5,− 4) −→ [4,4] = AB = [5 − xA ,− 4− yA] ⇒ A = (xA ,yA ) = (1,− 8) −→ [4,4] = DC = [3 − x ,6 − y ] ⇒ D = (x ,y ) = (− 1,2). D D D D](https://img.zadania.info/zad/7923031/HzadR9x.gif)
Piszemy teraz równanie prostej 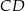 . Szukamy prostej w postaci
. Szukamy prostej w postaci 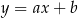 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 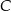 i
i 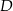 .
.
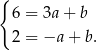
Odejmujemy od pierwszego równania drugie i mamy
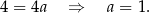
Stąd 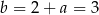 i prosta
i prosta 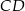 ma równanie
ma równanie 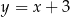 . Wysokość
. Wysokość 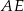 jest prostopadła do tej prostej, więc ma równanie postacie
jest prostopadła do tej prostej, więc ma równanie postacie 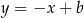 . Współczynnik
. Współczynnik 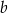 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 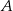 .
.

Prosta 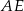 ma więc równanie
ma więc równanie 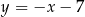 . Szukamy teraz jej punktu wspólnego
. Szukamy teraz jej punktu wspólnego 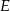 z prostą
z prostą 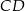 .
.
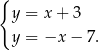
Dodajemy równania stronami i mamy 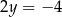 , czyli
, czyli 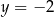 . Stąd
. Stąd 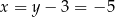 i
i 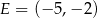 .
.
Odpowiedź: