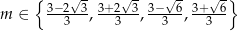Zadanie nr 9070956
Dany jest równoległobok, którego boki zawierają się w prostych o równaniach: 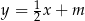 ,
, 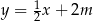 ,
, 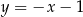 ,
, 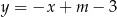 , gdzie
, gdzie 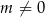 i
i 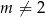 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 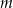 , dla których iloczyn długości dwóch wysokości tego równoległoboku, które nie są równoległe, jest równy
, dla których iloczyn długości dwóch wysokości tego równoległoboku, które nie są równoległe, jest równy 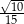 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
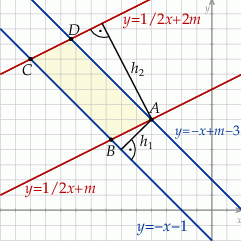
Zauważmy, że łatwo jest wyznaczyć współrzędne jednego z wierzchołków, powiedzmy 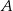 , danego równoległoboku – znajdźmy punkt wspólny prostych
, danego równoległoboku – znajdźmy punkt wspólny prostych 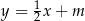 i
i 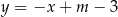 .
.

Stąd
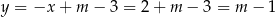
i 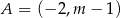 .
.
Obliczamy najpierw odległość tego punktu od prostej 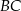 :
: 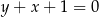 :
:
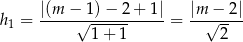
Teraz obliczamy odległość punktu 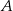 od prostej
od prostej 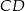 :
: 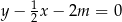 .
.
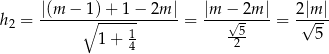
Pozostało teraz rozwiązać równanie
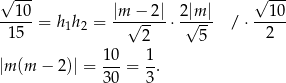
Jeżeli 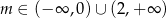 , to mamy równanie
, to mamy równanie
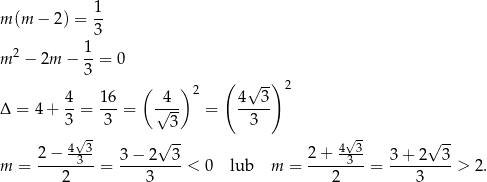
Jeżeli natomiast 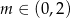 , to mamy równanie
, to mamy równanie
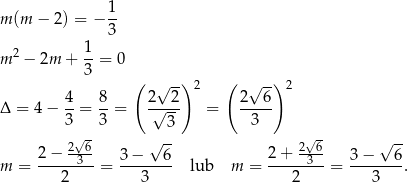
Łatwo sprawdzić, że oba te rozwiązania spełniają warunek 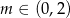 . W sumie są więc cztery wartości parametru
. W sumie są więc cztery wartości parametru 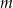 spełniające warunki zadania:
spełniające warunki zadania:
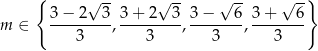
Odpowiedź: