/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt/Równoległobok

Zadanie nr 9883571

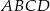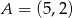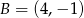Pole równoległoboku ABCD o danych wierzchołkach A = (5 ,2) i B = (4,− 1) jest równe 26. Wyznacz współrzędne pozostałych wierzchołków równoległoboku, jeżeli jego przekątne przecinają się w punkcie leżącym na prostej 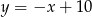y = −x + 10 , który ma obie współrzędne będące liczbami całkowitymi.

Wersja PDF

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

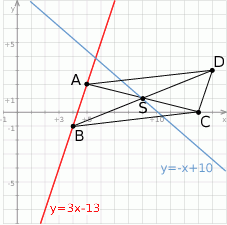
Zauważmy, że przekątne dzielą równoległobok na cztery trójkąty o równych polach (bo przekątne dzielą się na połowy), zatem pole trójkąta 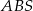ABS jest równe 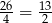26 = 13 4 2 . Wiemy ponadto, że punkt 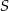S leży na prostej 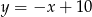y = −x + 10 , więc ma on współrzędne postaci 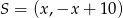S = (x ,−x + 10) . Zajmiemy się teraz wyznaczeniem punktu S .

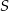Sposób I

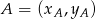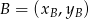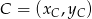Korzystamy ze wzoru na pole trójkąta o wierzchołkach A = (x ,y ) A A , B = (xB,yB ) i C = (xC ,yC) .

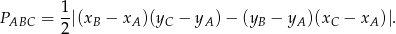
1 PABC = --|(xB − xA)(yC − yA) − (yB − yA )(xC − xA )|. 2

W naszej sytuacji (stosujemy wzór dla 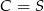C = S ) mamy

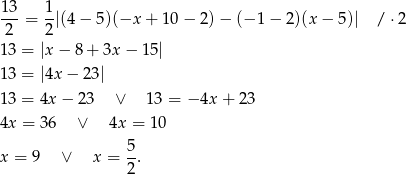
1 3 1 -2- = 2-|(4 − 5)(−x + 1 0− 2)− (− 1 − 2)(x − 5 )| /⋅ 2 13 = |x − 8 + 3x − 15| 13 = |4x − 23| 13 = 4x − 23 ∨ 13 = − 4x+ 23 4x = 36 ∨ 4x = 10 5 x = 9 ∨ x = -. 2

Wiemy, że punkt 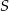S ma obie współrzędne całkowite, więc musi być 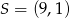S = (9,1) . Pozostałe wierzchołki równoległoboku wyznaczamy korzystając z tego, że punkt 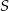S jest środkiem przekątnych 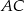AC i BD .

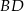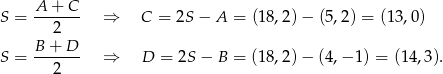
A--+-C- S = 2 ⇒ C = 2S − A = (18,2) − (5,2) = (1 3,0) B + D S = ------- ⇒ D = 2S − B = (18,2) − (4,− 1) = (1 4,3). 2

Sposób II

Tym razem obliczymy pole trójkąta wprost, ze wzoru 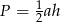1 P = 2ah . Liczymy długość podstawy trójkąta

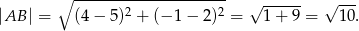
∘ --------------------- √ ------ √ --- |AB | = (4− 5 )2 + (− 1 − 2)2 = 1 + 9 = 10.

To pozwala obliczyć długość wysokości 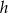h trójkąta 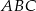ABC opuszczonej na bok AB .

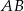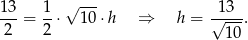
13 1 √ --- 13 ---= --⋅ 10 ⋅h ⇒ h = √---. 2 2 10

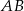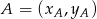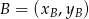Teraz będziemy chcieli skorzystać ze wzoru na odległość punktu od prostej. Zanim to jednak zrobimy, napiszmy równanie prostej AB . Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty A = (xA ,yA) i B = (x ,y ) B B :

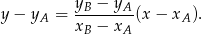
y − yA = yB-−--yA(x − xA ). xB − xA

W naszej sytuacji mamy

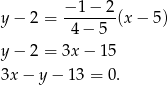
y − 2 = −-1-−-2(x − 5) 4 − 5 y − 2 = 3x − 15 3x − y− 13 = 0.

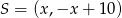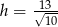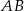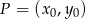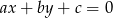Wiemy, że punkt S = (x,−x + 10) leży w odległości 13 h = √10- od prostej AB . Zapiszmy ten warunek korzystając ze wzoru na odległość punktu P = (x ,y ) 0 0 od prostej ax + by + c = 0 :

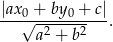
|ax0 + by 0 + c| ---√-----------. a2 + b2

W naszej sytuacji mamy

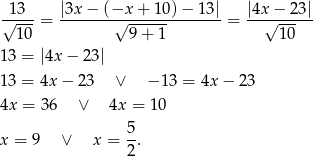
13 |3x − (−x + 10)− 13| |4x − 23| √----= -------√--------------= ---√----- 10 9 + 1 10 13 = |4x − 23| 13 = 4x − 23 ∨ −1 3 = 4x − 23 4x = 36 ∨ 4x = 10 x = 9 ∨ x = 5. 2

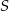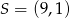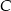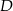Współrzędne punktu S są liczbami całkowitymi, więc S = (9,1) . Współrzędne punktów C i D wyznaczamy tak samo jak w pierwszym sposobie.  
Odpowiedź: C = (13,0),D = (14 ,3)

Wersja PDF