/Szkoła średnia/Prawdopodobieństwo/Z definicji/Karty

Zadanie nr 4118340

Z talii 52 kart losujemy bez zwracania dwie karty. Jakie jest prawdopodobieństwo wylosowania asa i króla?

Wersja PDF

Rozwiązanie

Sposób I

Przyjmijmy za zdarzenia elementarne dwuelementowe zbiory wylosowanych kart. Mamy zatem

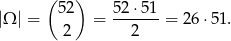
( ) |Ω | = 52 = 52⋅-51-= 26 ⋅51. 2 2

Zarówno asa, jak i króla, możemy wybrać na 4 sposoby, więc jest

4 ⋅4 = 16

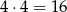
zdarzeń sprzyjających. Zatem prawdopodobieństwo wynosi

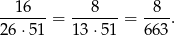
--16---= --8----= -8-. 26 ⋅51 13 ⋅51 663

Sposób II

Tym razem za zdarzenia elementarne przyjmijmy uporządkowane pary wylosowanych kart. Ponieważ losujemy bez zwracania mamy

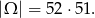
|Ω | = 52 ⋅51.

Zarówno asa, jak i króla, możemy wybrać na 4 sposoby. Dodatkowo jednak musimy ustalić czy na pierwszym miejscu jest as, czy król. To podwaja ilość zdarzeń sprzyjających, czyli

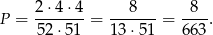
2 ⋅4 ⋅4 8 8 P = ------- = -------= ----. 5 2⋅5 1 13⋅5 1 66 3

 
Odpowiedź: 8 663

Wersja PDF