/Szkoła średnia/Prawdopodobieństwo/Z definicji/Karty

Zadanie nr 5388889

Wybieramy trzy karty z talii 24 kart, składającej się ze wszystkich figur oraz dziewiątek i dziesiątek. Jakie jest prawdopodobieństwo, że wśród tych kart jest co najmniej jeden as.

Wersja PDF

Rozwiązanie

Jeżeli ustalimy, że zdarzenia sprzyjające to nieuporządkowane trójki wylosowanych kart to

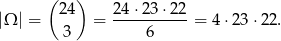
( ) |Ω | = 24 = 24-⋅23-⋅22-= 4⋅ 23⋅2 2. 3 6

Prościej jest policzyć ilość zdarzeń, w których nie ma asa:

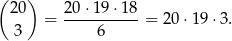
( ) 20 20-⋅19-⋅18- 3 = 6 = 20⋅1 9⋅3.

Zatem prawdopodobieństwo zdarzenia przeciwnego wynosi

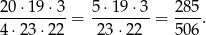
20-⋅19-⋅3 5⋅19-⋅3- 285- 4 ⋅23⋅ 22 = 23 ⋅22 = 506 .

Szukane prawdopodobieństwo wynosi

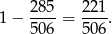
2-85 2-21 1 − 5 06 = 5 06.

 
Odpowiedź: 221 506

Wersja PDF