/Szkoła średnia/Prawdopodobieństwo/Z definicji/Karty

Zadanie nr 7620811

Dodaj do ulubionych
Dodaj do rozwiązanych
  • Na ile sposobów można ze standardowej talii 52 kart wybrać 13 kart tak, aby mieć co najwyżej jednego czerwonego (kier lub karo) asa?
  • Jakie jest prawdopodobieństwo takiego zdarzenia?

Rozwiązanie

  •  

    Sposób I

    Możliwe są dwie sytuacje: w wybranych kartach jest dokładnie jeden czerwony as, lub nie ma żadnego czerwonego asa. W drugim przypadku jest

    ( ) 5 0 1 3

    możliwości (wybieramy 13 kart, wśród których nie ma czerwonego asa).

    W pierwszej sytuacji na dwa sposoby możemy wybrać czerwonego asa, a potem na

    ( ) 5 0 1 2

    sposobów dobieramy do niego 12 dodatkowych kart.

    Sposób II

    Zauważmy, że łatwo jest obliczyć, ile jest złych wyborów: musimy wybrać 2 czerwone asy, a potem dobrać do nich 11 innych kart. W sumie jest więc 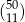(5101) złych wyborów. W takim razie dobrych wyborów jest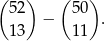

    ( 52) (5 0) − . 13 1 1

     
    Odpowiedź: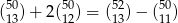 (50) + 2(50) = (52)− (50) 13 12 13 11

  •  

    Sposób I

    Wszystkich możliwych wyborów 13 kart jest 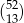(52) 13 , wiec prawdopodobieństwo jest równe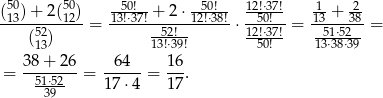

    50 50 50! 50! 12!⋅37! 1 2 (13)-+-2(12) -13!⋅37! +-2⋅-12!⋅38!- --50!-- 13-+-38- (52) = -52!-- ⋅12!⋅37!= --51⋅52- = 13 13!⋅39! 50! 13⋅38⋅39 38+--26- -64--- 16- = 51⋅52 = 17⋅ 4 = 17 . 39

    Sposób II

    Tym razem korzystamy z drugiej postaci odpowiedzi w poprzednim podpunkcie.

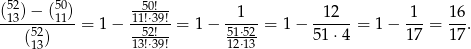
    52 50 (13)-−-(11) 115!0⋅3!9! --1-- --12-- 1-- 16- 52 = 1 − --52!- = 1 − 51⋅52 = 1 − 51 ⋅4 = 1− 17 = 17. (13) 13!⋅39! 12⋅13

     
    Odpowiedź: 16 17

Wersja PDF