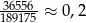/Szkoła średnia/Prawdopodobieństwo/Z definicji/Karty

Zadanie nr 8630447

Oblicz prawdopodobieństwo otrzymania przez brydżystę dokładnie jednego asa i dokładnie jednego króla.

Wersja PDF

Rozwiązanie

Talia kart składa się z 52 kart, a brydżysta otrzymuje 13 z nich. Jeżeli przyjmiemy za zdarzenia elementarne zbiory otrzymanych kart to mamy

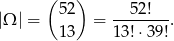
( ) |Ω | = 52 = --52!--. 13 13!⋅39 !

Zarówno asa, jak i króla możemy wybrać na 4 sposoby. Do tego musimy dobrać 11 kart. Możemy to zrobić na

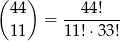
( ) 44 --44!--- 11 = 11!⋅33 !

sposobów. Zatem prawdopodobieństwo wynosi

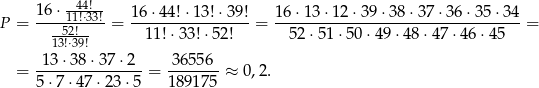
16 ⋅-44!-- 16 ⋅44!⋅1 3!⋅39! 16⋅ 13⋅1 2⋅39 ⋅38 ⋅37 ⋅36 ⋅35 ⋅34 P = ----1521!!⋅33!= -----------------= ----------------------------------= 13!⋅39! 11!⋅ 33!⋅52! 52⋅5 1⋅5 0⋅49 ⋅48 ⋅47 ⋅46 ⋅45 13 ⋅38⋅ 37⋅2 36556 = ---------------= ------- ≈ 0,2 . 5 ⋅7⋅4 7⋅2 3⋅5 1891 75

 
Odpowiedź: 13869551675 ≈ 0,2

Wersja PDF