Zadanie nr 1033926
Zdarzenia losowe 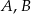 są zawarte w
są zawarte w 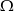 oraz
oraz 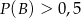 . Wykaż, że
. Wykaż, że
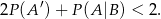
Rozwiązanie
Nierówność, którą mamy udowodnić może zapisać w postaci
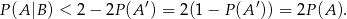
Zauważmy teraz, że
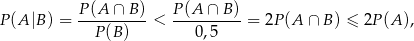
bo 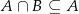 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Zdarzenia losowe 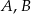 są zawarte w
są zawarte w 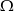 oraz
oraz 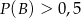 . Wykaż, że
. Wykaż, że
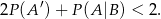
Nierówność, którą mamy udowodnić może zapisać w postaci
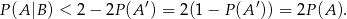
Zauważmy teraz, że
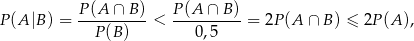
bo 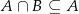 .
.
