/Szkoła średnia/Prawdopodobieństwo/Bez treści

Zadanie nr 2749712

Dodaj do ulubionych
Dodaj do rozwiązanych

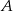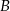Wiadomo, że zdarzenia A i B są niezależne oraz 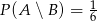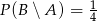1 P (A ∖ B) = 6 , 1 P (B ∖ A ) = 4 . Oblicz P (A ∪ B ) .

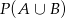Rozwiązanie

Narysujmy sobie diagram Venna.

PIC

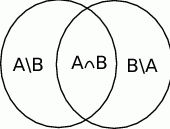
Z obrazka widać, że

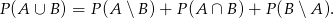
P (A ∪ B) = P(A ∖ B) + P (A ∩ B )+ P (B ∖A ).

Widać, że musimy wyliczyć 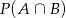P(A ∩ B) . Tu korzystamy z niezależności.

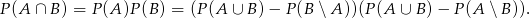
P(A ∩ B) = P (A )P(B) = (P(A ∪ B )− P(B ∖ A ))(P(A ∪ B )− P(A ∖ B )).

Jeżeli oznaczymy 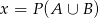x = P (A ∪ B ) to mamy równanie

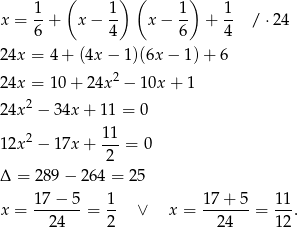
1 ( 1) ( 1) 1 x = --+ x − -- x− -- + -- / ⋅24 6 4 6 4 24x = 4 + (4x − 1)(6x− 1)+ 6 2 24x = 1 0+ 2 4x − 10x + 1 24x2 − 34x + 11 = 0 12x2 − 17x + 11-= 0 2 Δ = 2 89− 264 = 25 x = 17-−-5-= 1- ∨ x = 17-+-5-= 11-. 24 2 24 12

 
Odpowiedź: 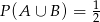P (A ∪ B) = 12 lub P (A ∪ B ) = 1112

Wersja PDF