Zadanie nr 5438832
Niech 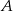 ,
, 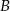 będą zdarzeniami o prawdopodobieństwach
będą zdarzeniami o prawdopodobieństwach 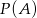 i
i 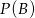 . Wykaż, że jeżeli
. Wykaż, że jeżeli 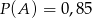 i
i 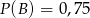 , to prawdopodobieństwo warunkowe spełnia nierówność
, to prawdopodobieństwo warunkowe spełnia nierówność 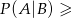 0,8.
0,8.
Rozwiązanie
Sprawdźmy najpierw co musimy udowodnić. Korzystając ze wzoru na prawdopodobieństwo warunkowe mamy:
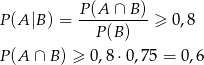
Korzystamy teraz ze wzoru 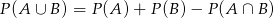 .
.
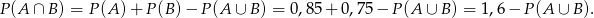
Zatem nierówność, którą mamy udowodnić ma postać
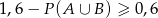
czyli 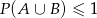 , a ta nierówność jest oczywiście zawsze spełniona. Żeby dostać teraz porządne rozwiązanie (np. gdybyśmy rozwiązywali to zadanie na maturze), powinniśmy przepisać powyższe przekształcenia od końca, tzn. startujemy od
, a ta nierówność jest oczywiście zawsze spełniona. Żeby dostać teraz porządne rozwiązanie (np. gdybyśmy rozwiązywali to zadanie na maturze), powinniśmy przepisać powyższe przekształcenia od końca, tzn. startujemy od 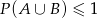 , potem ze wzoru zamieniamy
, potem ze wzoru zamieniamy 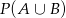 na
na 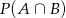 itd.
itd.

