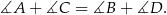Zadanie nr 2302763
W czworokącie 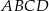 spełniony jest warunek
spełniony jest warunek 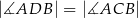 . Wykaż, że na czworokącie
. Wykaż, że na czworokącie 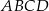 można opisać okrąg.
można opisać okrąg.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
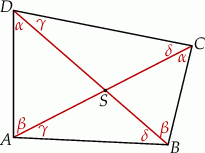
Czworokąt jest wpisany w okrąg, jeżeli sumy miar jego przeciwległych kątów są równe. Spróbujemy pokazać, że tak jest w naszej sytuacji.
Zauważmy, że podana równość kątów oznacza, że trójkąty 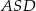 i
i 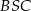 są podobne (bo trójkąty te mają dwa takie same kąty:
są podobne (bo trójkąty te mają dwa takie same kąty: 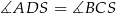 , oraz kąt przy wierzchołku
, oraz kąt przy wierzchołku 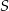 ). W szczególności
). W szczególności 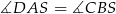 oraz
oraz
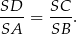
Jeżeli zapiszemy powyższą równość w postaci
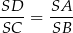
i popatrzymy na trójkąty 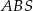 i
i 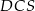 to widać, że są one podobne (mają wspólny kąt przy wierzchołku
to widać, że są one podobne (mają wspólny kąt przy wierzchołku 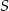 i proporcjonalne boki wychodzące z tego wierzchołka). Zatem
i proporcjonalne boki wychodzące z tego wierzchołka). Zatem 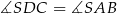 oraz
oraz 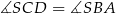 . Wykazaliśmy zatem, że rzeczywiście
. Wykazaliśmy zatem, że rzeczywiście