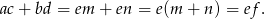Zadanie nr 2826507
Udowodnij, że w czworokącie wpisanym w okrąg suma iloczynów długości przeciwległych boków jest równa iloczynowi długości przekątnych (twierdzenie Ptolemeusza).
Rozwiązanie
Zaczynamy od szkicowego rysunku.
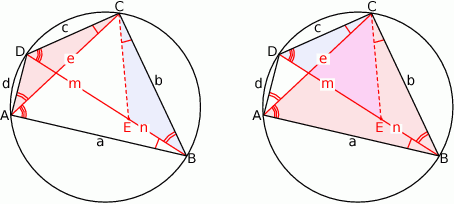
Niech 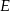 będzie takim punktem przekątnej
będzie takim punktem przekątnej 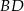 , że
, że 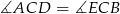 oraz oznaczmy
oraz oznaczmy 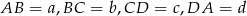 ,
, 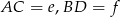 ,
, 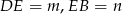 .
.
Zauważmy najpierw, że trójkąty 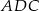 i
i 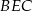 mają równe kąty (bo
mają równe kąty (bo 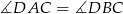 ), więc są podobne. Mamy zatem
), więc są podobne. Mamy zatem
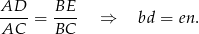
Podobnie, trójkąty 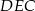 i
i 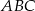 mają równe kąty (
mają równe kąty (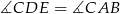 ,
, 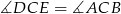 ), więc są podobne. Mamy stąd
), więc są podobne. Mamy stąd
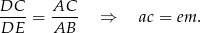
Dodajemy teraz dwie otrzymane równości stronami