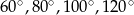/Konkursy/Zadania/Geometria/Planimetria/Czworokąt/Wpisany w okrąg

Zadanie nr 9449442

Dodaj do ulubionych
Dodaj do rozwiązanych

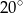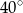Przedłużenia przeciwległych boków czworokąta wpisanego w okrąg tworzą kąty ostre o miarach 20 ∘ i 40∘ . Oblicz miary kątów czworokąta.

Rozwiązanie

Zacznijmy od rysunku i oznaczmy kąty czworokąta przez 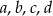a ,b ,c,d jak na rysunku.

PIC

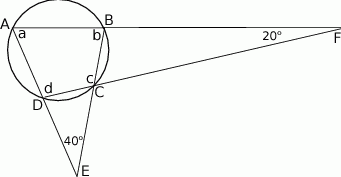
Ponieważ czworokąt jest wpisany w okrąg, to sumy przeciwległych kątów są sobie równe, czyli

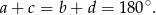
a + c = b + d = 180∘.

Ponadto, z trójkątów ABE i AF D mamy

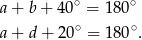
∘ ∘ a + b + 40 = 180 a + d + 20∘ = 180∘.

Dodając te dwie równości stronami mamy

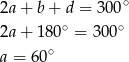
2a + b + d = 3 00∘ ∘ ∘ 2a + 180 = 300 a = 60 ∘

Stąd łatwo wyliczamy 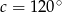c = 120∘ , b = 80∘ , d = 100∘ .  
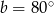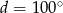Odpowiedź: ∘ ∘ ∘ ∘ 60 ,80 ,100 ,12 0

Wersja PDF