/Szkoła średnia/Ciągi/Geometryczny

Zadanie nr 1034303

Dodaj do ulubionych
Dodaj do rozwiązanych

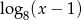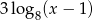Wyznacz liczbę x tak, aby liczby dodatnie log 8(x− 1) , 3 lo g8(x− 1) , 6 tworzyły ciąg geometryczny (w podanej kolejności).

Rozwiązanie

Jeżeli liczby te mają być dodatnie, to musi być 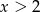x > 2 .

Sposób I

Jeżeli trzy liczby 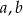a,b i c są kolejnymi wyrazami ciągu geometrycznego, to

2 b = ac.

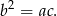
Mamy zatem

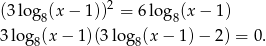
(3log (x − 1 ))2 = 6log (x − 1 ) 8 8 3log8(x − 1 )(3log8(x − 1) − 2) = 0 .

Ponieważ założyliśmy, że 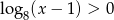log8(x − 1) > 0 , mamy stąd

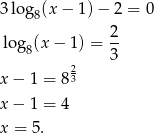
3 log8(x − 1) − 2 = 0 2 lo g8(x − 1) = -- 2 3 x − 1 = 83 x − 1 = 4 x = 5.

Sposób II

Ponieważ druga z liczb jest 3 razy większa od pierwszej, to szukany ciąg musi mieć iloraz 3. W takim razie mamy równanie

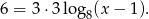
6 = 3 ⋅3log (x − 1). 8

rozwiązujemy je dokładnie tak samo jak w I sposobie.  
Odpowiedź: x = 5

Wersja PDF