Zadanie nr 1433905
Wyznacz wszystkie ciągi geometryczne o wyrazach różnych od zera, w których każdy wyraz, rozpoczynając od wyrazu trzeciego, jest równy średniej arytmetycznej dwóch poprzednich wyrazów.
Rozwiązanie
Powiedzmy, że nasz ciąg to 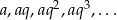 . Zauważmy najpierw, że wystarczy aby podany warunek był spełniony dla wyrazu trzeciego, a wtedy automatycznie jest spełniony dla wszystkich następnych wyrazów. Rzeczywiście, jeżeli
. Zauważmy najpierw, że wystarczy aby podany warunek był spełniony dla wyrazu trzeciego, a wtedy automatycznie jest spełniony dla wszystkich następnych wyrazów. Rzeczywiście, jeżeli
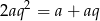
to mnożąc tę równość przez 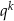 mamy
mamy
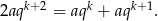
Pozostaje sprawdzić kiedy
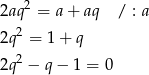
Liczymy 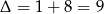 ,
, 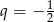 lub
lub 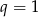 . Zatem dowolny ciąg
. Zatem dowolny ciąg 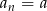 lub
lub 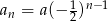 , gdzie
, gdzie 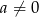 spełnia warunki zadania.
spełnia warunki zadania.
Odpowiedź: 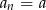 lub
lub 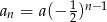 , gdzie
, gdzie