/Szkoła średnia/Ciągi/Geometryczny

Zadanie nr 2080595

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest ciąg geometryczny 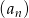(an) o pierwszym wyrazie równym 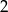2 , i ilorazie równym 10. Wykaż, że wszystkie punkty o współrzędnych 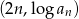(2n ,lo gan) leżą na jednej prostej.

Rozwiązanie

Wyraz ogólny podanego ciągu to 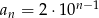n−1 an = 2⋅10 . Stąd intersujące nas punkty mają współrzędne

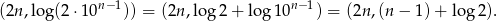
(2n,log(2 ⋅10n −1)) = (2n,log 2 + log 10n−1) = (2n ,(n− 1)+ lo g2).

Sposób I

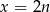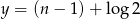Najprostszy sposób wykazania, że punkty te istotnie leżą na jednej prostej, to napisanie równania prostej, do której te punkty należą. Jeżeli oznaczymy x = 2n i y = (n − 1)+ log 2 , to

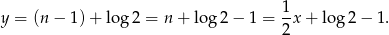
1 y = (n − 1)+ lo g2 = n+ lo g2 − 1 = -x + log 2− 1. 2

Otrzymana prosta przechodzi przez wyszystkie wyrazy ciągu 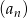(a ) n .

Sposób II

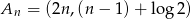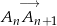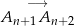Inny sposób wykazania, że punkty A = (2n,(n − 1) + log 2) n leżą na jednej prostej, to wykazanie, że wektory −→ AnAn + 1 i −→ An +1An +2 są równoległe dla n ≥ 1 . Liczymy

A −A→ = [2(n + 1) − 2n ,n− (n− 1)] = [2,1] n n+1 − → −→ An+ 1An +2 = [2(n + 2) − 2(n + 1 ),(n + 1)− n ] = [2 ,1] = AnAn + 1.
Wersja PDF