Zadanie nr 2381110
Pierwszy wyraz niemonotonicznego ciągu geometrycznego 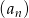 jest równy 48 i jest o 36 większy od wyrazu trzeciego.
jest równy 48 i jest o 36 większy od wyrazu trzeciego.
- Oblicz iloraz ciągu
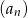 .
. - Oblicz ósmy wyraz ciągu
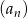 .
. - Suma kilku początkowych wyrazów ciągu
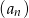 jest równa
jest równa 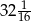 . Oblicz, ile wyrazów zsumowano.
. Oblicz, ile wyrazów zsumowano.
Rozwiązanie
- Jeżeli ciąg jest niemonotoniczny, to
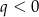 . Wiemy, że
. Wiemy, że 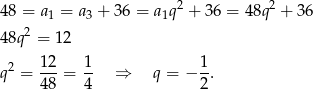
Odpowiedź: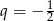
- Liczymy
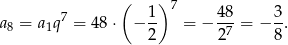
Odpowiedź: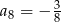
- Mamy równanie
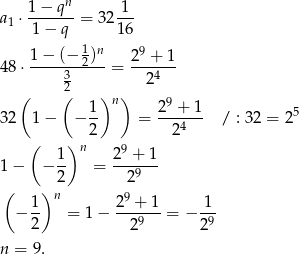
Odpowiedź: Dziewięć wyrazów.

