Zadanie nr 2882690
O trapezie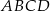 
wiadomo, że można w niego wpisać okrąg, a ponadto długości jego boków 
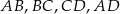– w podanej kolejności – tworzą ciąg geometryczny. Uzasadnij, że trapez 
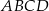jest rombem.
Rozwiązanie
Szkicujemy trapez.
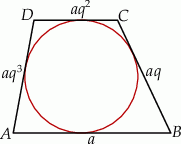
Ponieważ długości boków trapezu tworzą ciąg geometryczny, to możemy je oznaczyć przez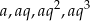 
dla pewnych 
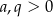. Ponieważ w trapez można wpisać okrąg, to sumy przeciwległych boków są sobie równe. Mamy zatem
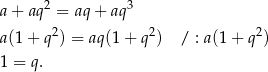
To oznacza, że wszystkie boki czworokąta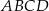 
mają tę samą długość, czyli jest to romb.
Zauważmy, że w rozwiązaniu nie miało żadnego znaczenia, że czworokąt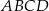 
jest trapezem.
