/Szkoła średnia/Ciągi/Geometryczny

Zadanie nr 4210346

Dodaj do ulubionych
Dodaj do rozwiązanych

Ciąg geometryczny 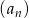(an ) ma 100 wyrazów i są one liczbami dodatnimi. Suma wszystkich wyrazów o numerach nieparzystych jest sto razy większa od sumy wszystkich wyrazów o numerach parzystych oraz

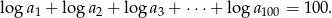
log a1 + lo ga2 + log a3 + ⋅ ⋅⋅+ log a100 = 100.

Oblicz 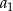a1 .

Rozwiązanie

Rozszyfrujmy pierwszą z podanych informacji.

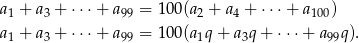
a + a + ⋅⋅⋅+ a = 100(a + a + ⋅⋅⋅+ a ) 1 3 99 2 4 100 a1 + a3 + ⋅⋅⋅+ a99 = 100(a1q + a3q + ⋅⋅⋅ + a99q).

Ponieważ wyrazy ciągu są liczbami dodatnimi możemy obie strony podzielić przez 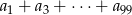a + a + ⋅⋅⋅ + a 1 3 99 i otrzymujemy

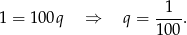
-1-- 1 = 1 00q ⇒ q = 100.

Teraz próbujemy rozszyfrować drugą z podanych informacji. Zanim to jednak zrobimy zauważmy, że

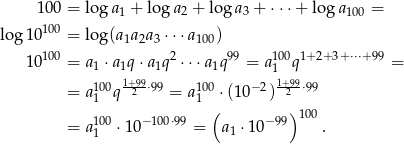
1 00 = log a1 + log a2 + loga 3 + ⋅⋅⋅ + log a100 = 100 log 10 = log(a1a2a3 ⋅⋅⋅a100) 10100 = a ⋅a q⋅a q2⋅⋅⋅a q99 = a 100q1+ 2+ 3+⋅⋅⋅+99 = 1 11+99 1 1 11+99 = a1100q-2-⋅99 = a1100⋅(1 0−2)-2--⋅99 ( )100 = a100⋅1 0−100⋅99 = a1 ⋅10 −99 . 1

Stąd

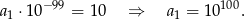
− 99 100 a1 ⋅10 = 10 ⇒ a1 = 10 .

 
Odpowiedź: 100 a1 = 1 0

Wersja PDF