Zadanie nr 4379947
Długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka tworzą ciąg geometryczny, w którym największy wyraz jest o 5 większy od wyrazu najmniejszego. Objętość prostopadłościanu jest równa 216. Oblicz długości krawędzi tego prostopadłościanu.
Rozwiązanie
Zaczynamy od rysunku
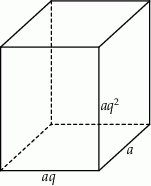
Niech  oznacza długość najkrótszej krawędzi. Wtedy pozostałe krawędzie mają długości
oznacza długość najkrótszej krawędzi. Wtedy pozostałe krawędzie mają długości 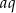 i
i 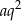 dla pewnego
dla pewnego 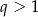 . Mamy podaną objętość prostopadłościanu, więc
. Mamy podaną objętość prostopadłościanu, więc
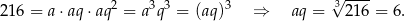
Ponadto
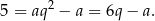
Podstawiamy teraz 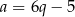 do równości
do równości 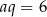 .
.
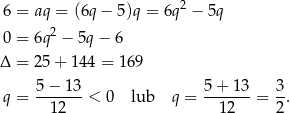
Pozostałe dwie krawędzie prostopadłościanu mają więc długości:
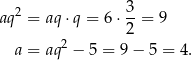
Odpowiedź: 4, 6, 9

