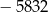/Szkoła średnia/Ciągi/Geometryczny

Zadanie nr 4710905

Dodaj do ulubionych
Dodaj do rozwiązanych

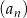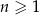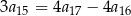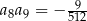Wyrazy niezerowego ciągu geometrycznego (an) , określonego dla n ≥ 1 spełniają warunki: 3a 15 = 4a17 − 4a16 oraz a8a 9 = − 5912 . Oblicz iloczyn pierwszych sześciu wyrazów tego ciągu.

Rozwiązanie

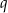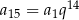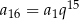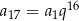Jeżeli oznaczymy przez q iloraz ciągu, to 14 a15 = a1q , 15 a16 = a1q i a17 = a1q 16 . Mamy zatem równanie

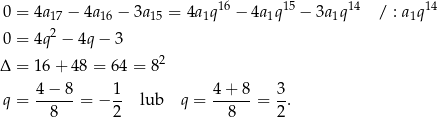
16 15 14 14 0 = 4a17 − 4a 16 − 3a 15 = 4a1q − 4a 1q − 3a 1q / : a1q 0 = 4q2 − 4q− 3 Δ = 16+ 48 = 64 = 82 4− 8 1 4 + 8 3 q = ------= − -- lub q = ------= -. 8 2 8 2

Zauważmy teraz, że jeżeli 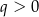q > 0 , to wszystkie wyrazy ciągu 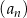(an) są tego samego znaku, a to byłoby sprzeczne z warunkiem 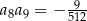a8a9 = − -9- 512 . W takim razie 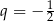1 q = − 2 oraz

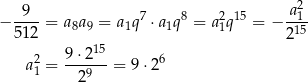
9 a2 − ----= a8a9 = a1q7 ⋅ a1q8 = a21q15 = −--1 512 215 2 9⋅-215 6 a1 = 29 = 9⋅ 2

Mamy zatem

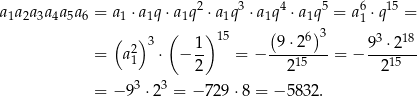
a1a2a3a4a5a 6 = a1 ⋅a1q ⋅a1q2 ⋅a1q3 ⋅ a1q4 ⋅a1q 5 = a61 ⋅q15 = ( ) ( )3 ( 2) 3 1- 15 -9-⋅26--- 93 ⋅-218 = a1 ⋅ − 2 = − 215 = − 215 3 3 = − 9 ⋅2 = −7 29⋅ 8 = − 5832.

 
Odpowiedź: − 5832

Wersja PDF