/Szkoła średnia/Ciągi/Geometryczny

Zadanie nr 6048852

Dodaj do ulubionych
Dodaj do rozwiązanych

Iloczyn piątego i jedenastego wyrazu ciągu geometrycznego o wyrazach dodatnich jest równy 4. Oblicz iloczyn piętnastu początkowych kolejnych wyrazów tego ciągu.

Rozwiązanie

Jeżeli dany ciąg to 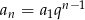n−1 an = a1q , to wiemy, że

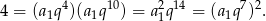
4 10 2 14 7 2 4 = (a1q )(a1q ) = a1q = (a 1q ) .

To co mamy obliczyć to

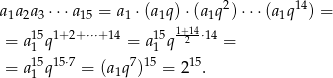
2 14 a1a2a3 ⋅⋅⋅a15 = a1 ⋅(a1q)⋅ (a 1q )⋅⋅⋅(a1q ) = 15 1+ 2+⋅⋅⋅+14 15 1+214⋅14 = a1 q = a1 q = = a115q15⋅7 = (a1q7)15 = 215.

 
Odpowiedź: 15 2 = 32 768

Wersja PDF