Zadanie nr 6541150
Udowodnij, że w ciągu geometrycznym 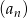 o wyrazach dodatnich iloczyn
o wyrazach dodatnich iloczyn 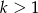 początkowych wyrazów ciągu jest równy
początkowych wyrazów ciągu jest równy 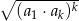 .
.
Rozwiązanie
Liczymy
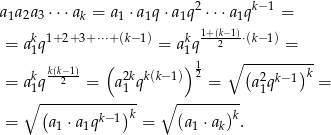
Po drodze skorzystaliśmy ze wzoru na sumę początkowych wyrazów ciągu arytmetycznego.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Udowodnij, że w ciągu geometrycznym 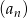 o wyrazach dodatnich iloczyn
o wyrazach dodatnich iloczyn 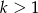 początkowych wyrazów ciągu jest równy
początkowych wyrazów ciągu jest równy 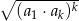 .
.
Liczymy
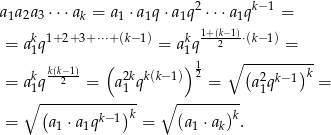
Po drodze skorzystaliśmy ze wzoru na sumę początkowych wyrazów ciągu arytmetycznego.
