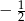Zadanie nr 6623498
Funkcje 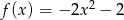 ,
, 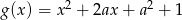 i
i 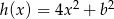 mają tę własność, że dla każdej liczby rzeczywistej
mają tę własność, że dla każdej liczby rzeczywistej  , liczby
, liczby 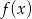 ,
,  i
i 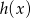 tworzą (w pewnej kolejności) ciąg geometryczny. Wyznacz możliwe ilorazy tego ciągu.
tworzą (w pewnej kolejności) ciąg geometryczny. Wyznacz możliwe ilorazy tego ciągu.
Rozwiązanie
Pierwszą rzeczą którą musimy zrobić, to ustalić w jakiej kolejności liczby te mogą tworzyć ciąg geometryczny. Sprawdzając 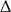 , widzimy, że
, widzimy, że 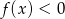 ,
, 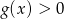 i
i 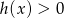 dla dowolnego
dla dowolnego  . Jeżeli liczby te mają tworzyć ciąg geometryczny, to musi być
. Jeżeli liczby te mają tworzyć ciąg geometryczny, to musi być 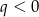 i
i 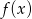 musi być środkowym wyrazem. Mamy zatem
musi być środkowym wyrazem. Mamy zatem
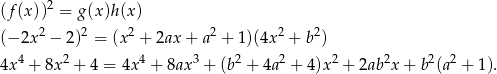
Mamy stąd układ równań
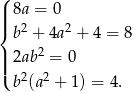
Z tego układu otrzymujemy 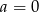 i
i 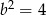 . Zatem podane funkcje to
. Zatem podane funkcje to 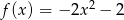 ,
, 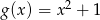 i
i 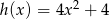 . Iloraz ciągu utworzonego przez te liczby to
. Iloraz ciągu utworzonego przez te liczby to 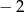 lub
lub 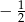 (zależy od tego czy ustawimy je w kolejności
(zależy od tego czy ustawimy je w kolejności 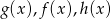 czy
czy 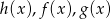 ).
).
Odpowiedź: -2 lub